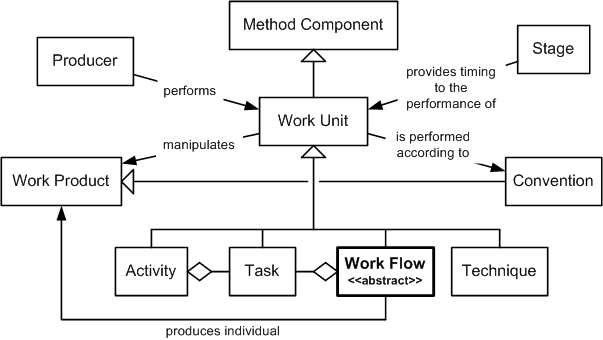
Work Flow
- Work Flow
- a work unit
that models a cohesive collection of
tasks
that either produces a new version of a single
work product
or provide a single service
As illustrated in the preceding figure, work flows are part of the following inheritance hierarchy:
- Type: Concrete
- Superclass: Work Unit
- Subclasses: None
- Example Instances:
- System requirements specification workflow
- Software architecture document workflow
- Human interface design document workflow
- Software component workflow
- Test case workflow
The typical responsibilities of workflows are to:
- Model the actual work done by producers to produce a new
version of a single work product.
- Document how work products are produced by collaborating producers.
- A workflow typically involves multiple collaborating producers performing multiple tasks.